LEA: Improving Sentence Similarity Robustness to Typos Using Lexical Attention Bias 论文阅读
KDD 2023 原文地址
Introduction
文本噪声,如笔误(Typos), 拼写错误(Misspelling)和缩写(abbreviations), 会影响基于 Transformer 的模型. 主要表现在两个方面:
- Transformer 的架构中不使用字符信息.
- 由噪声引起的词元分布偏移使得相同概念的词元更加难以关联.
先前解决噪声问题的工作主要依赖于数据增强策略, 主要通过在训练集中加入类似的 typos 和 misspelling 进行训练.
数据增强确实使得模型在损坏(噪声)样本上表现出出更高的鲁棒性.
虽然这种策略在一定程度上已被证明有效地缓解了词元分布偏移的问题, 但所有这些方法仍然受到在 词元化(tokenization)中字符信息会丢失的限制.
Approach
Self-attention
定义 self-attention 的输入为 \(X=\set{x_1, x_2, \dots, x_n}\), 输出为 \(Z=\set{z_1, z_2, \dots, z_n}\), 输出中的每个 token 的表示计算如下:
其中的注意力权重 \(a_{ij}\) 计算如下:
其中
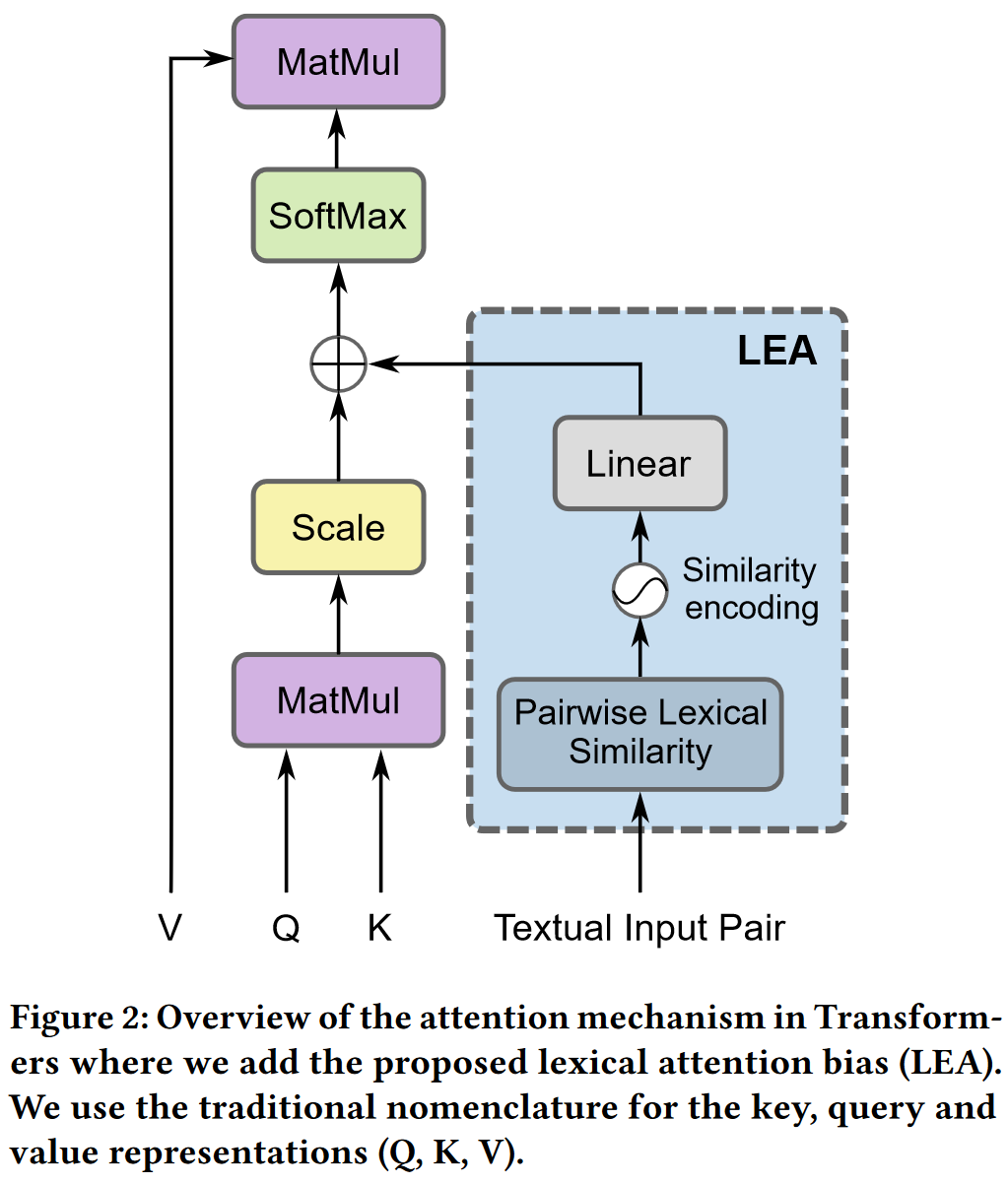
Lexical attention bias
对于语义文本相似性(textual similarity), 将两个句子拼接:
主要做法是参考了相对位置嵌入(relative position embeddings)的做法, 对 self-attention 中的 \(e_{ij}\) 进行如下修改:
其中第二项就是词偏向(lexical bias). \(W^L\in \mathbb R^{d^L\times 1}\) 是可训练参数, \(l\in \mathbb R^{1\times d^L}\) 是成对词汇注意嵌入(pairwise lexical attention embedding), \(\alpha\) 是一个固定的比例因子, 它在训练开始时根据两个项的大小自动计算一次.
为了计算成对词汇注意嵌入(pairwise lexical attention embedding), 先计算句子对之间单词的相似度, 而句子内单词的相似度设定为0:
其中 Sim 是一个度量, 用于表示两个单词之间的字符串相似度.
之后通过将将 \(s_{ij}\) 带入 Transformer 中的正余弦函数, 得到表示词相似度的 embedding:
最终的词相似度嵌入 \(l_{ij}\) 是上了两个向量的拼接.
Implementation details
论文中相似度度量选取的是 Jaccard 系数.
只在架构的后半层添加了 lexical attention bias.
Experiment
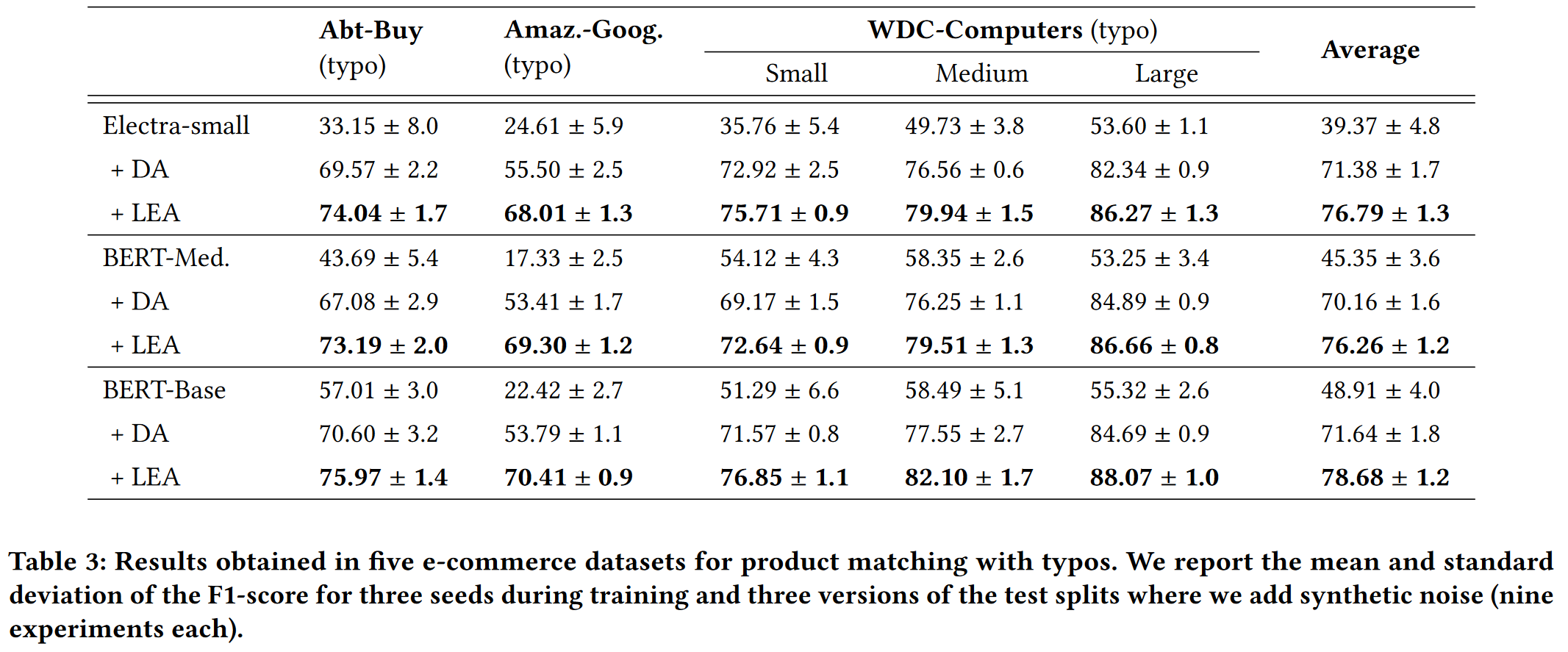
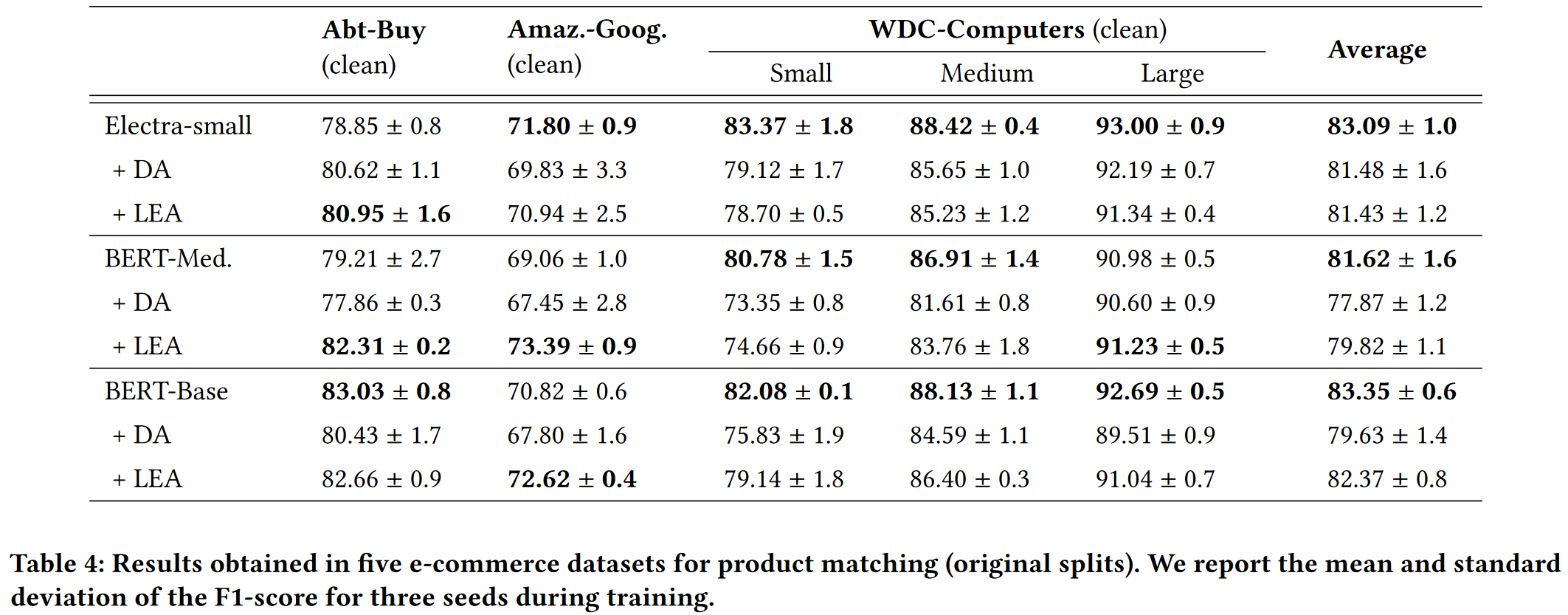
Performance
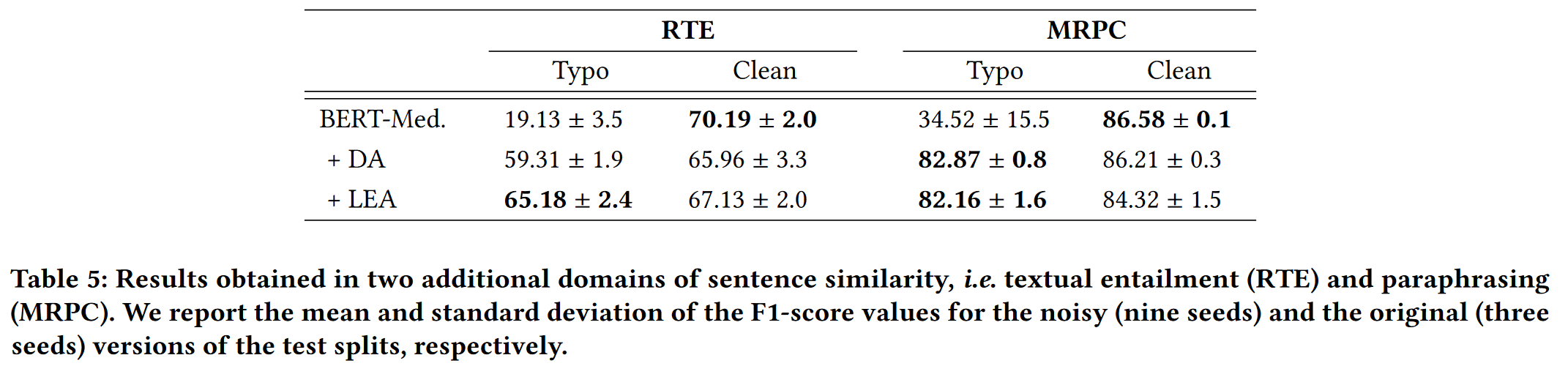
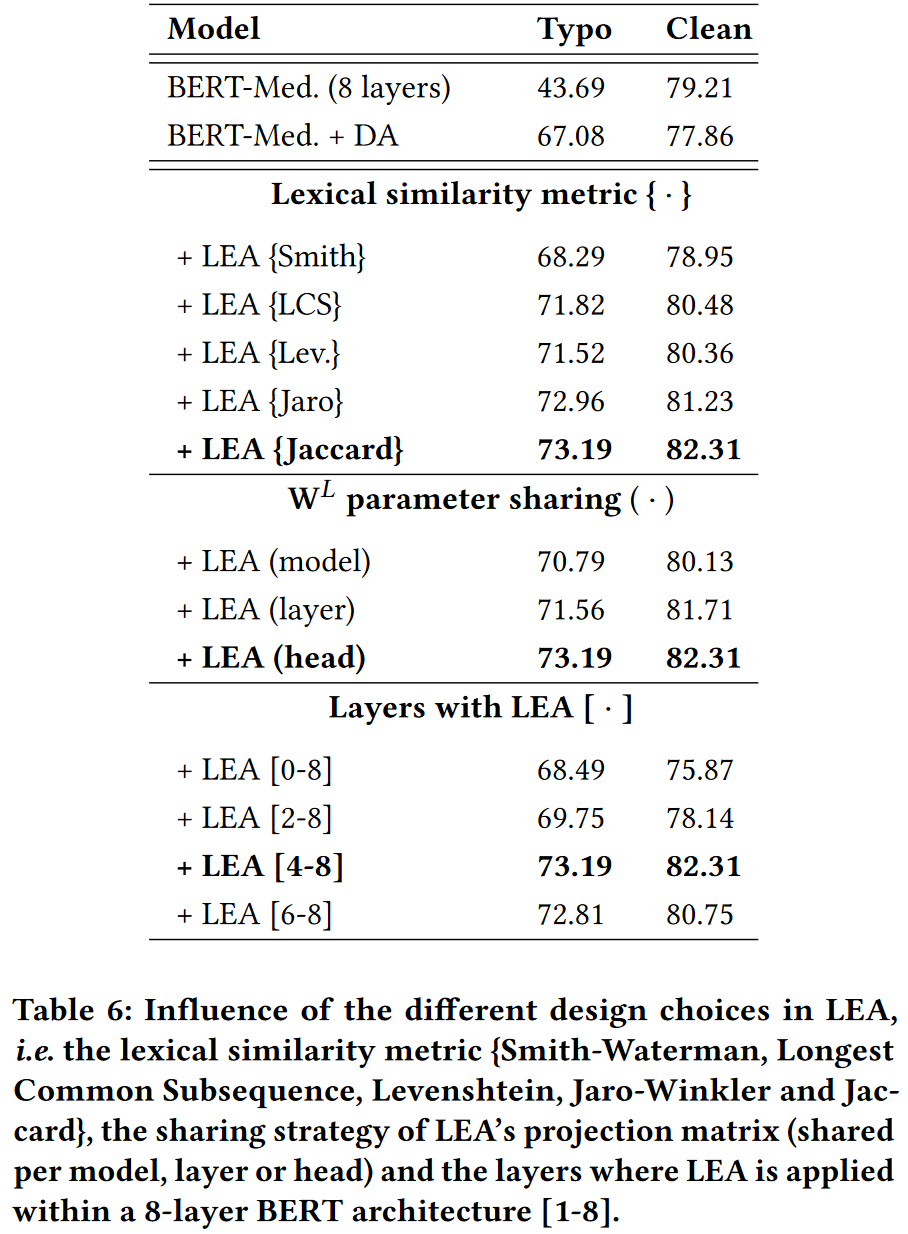
Impact of the lexical similarity choice
分析了使用不同相似度度量在 Abt-Buy 这个数据集上, BERT-Medium 的表现.
相似度度量包括: Jaccard (Jac.), Smith-Waterman (Smith), Longest Common Subsequence (LCS), Levenshtein (Lev.) and Jaro–Winkler (Jaro)
Jaccard 相似度系数是顺序不可知的, 因此对字符交换更健壮.
Jaccard 在有错别字和没有错别字的单词对之间提供了更高的可分离性, 这在短文本中是有益的.
然而, 随着句子长度的增加, 被比较的单词具有相似字符但含义不同的概率增加, 这降低了交换不变性优势.
Jaccard 相似系数: 集合 A, B 的交集与并集的比值
LEA on different layers and sharing strategy
文中认为, LEA 提供的字符级相似性可以被视为一种高级交互信息.
因此, 它为深层 Transformer 层补充了高层次的特性.
文中并没有验证这一假设.
Impact of the noise strength
直观地说, 由于 LEA 利用的字符级相似性不是在训练过程中学习到的, 因此它们为模型提供的信息在某种程度上较少依赖于噪声的量.
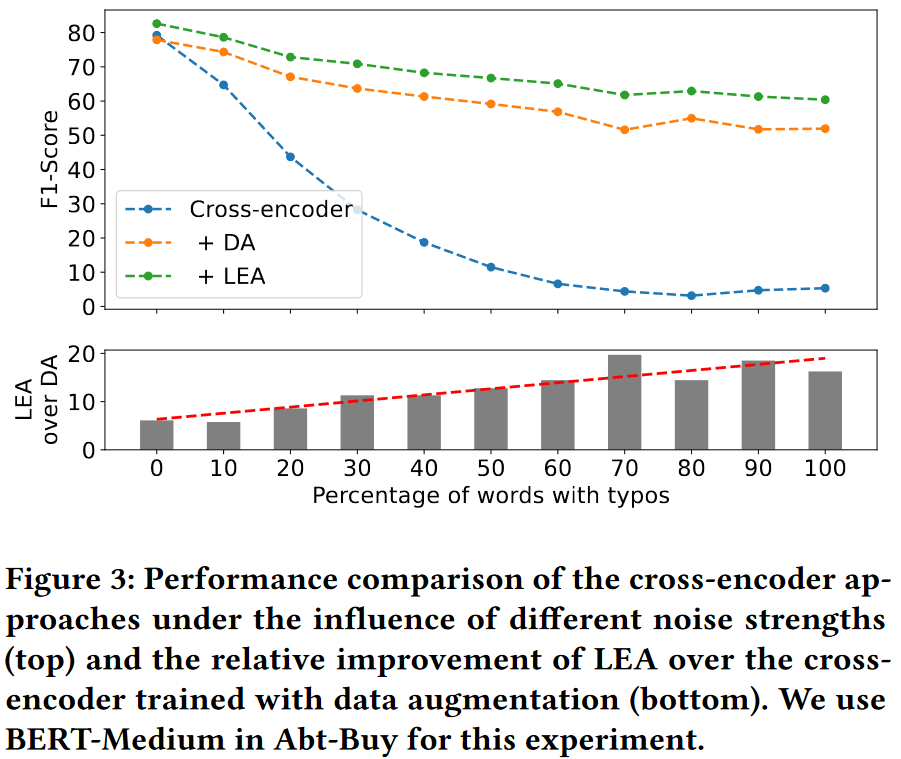
图3(下)显示了随着 typos 数量的增加, LEA 的性能与普通数据增强模型之间的差距越来越大, 这表明 LEA 可以更好地泛化到不同的噪声强度.
Additional experiments
Larger model
1.BERT-Large
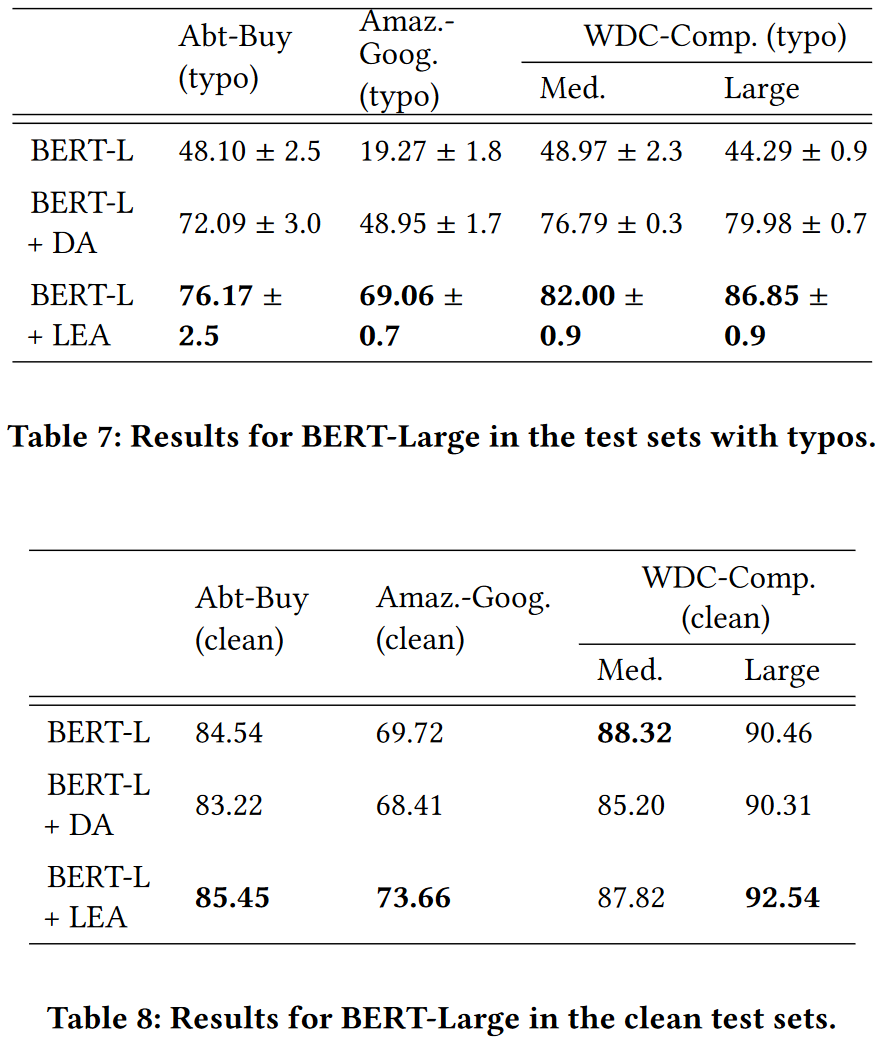
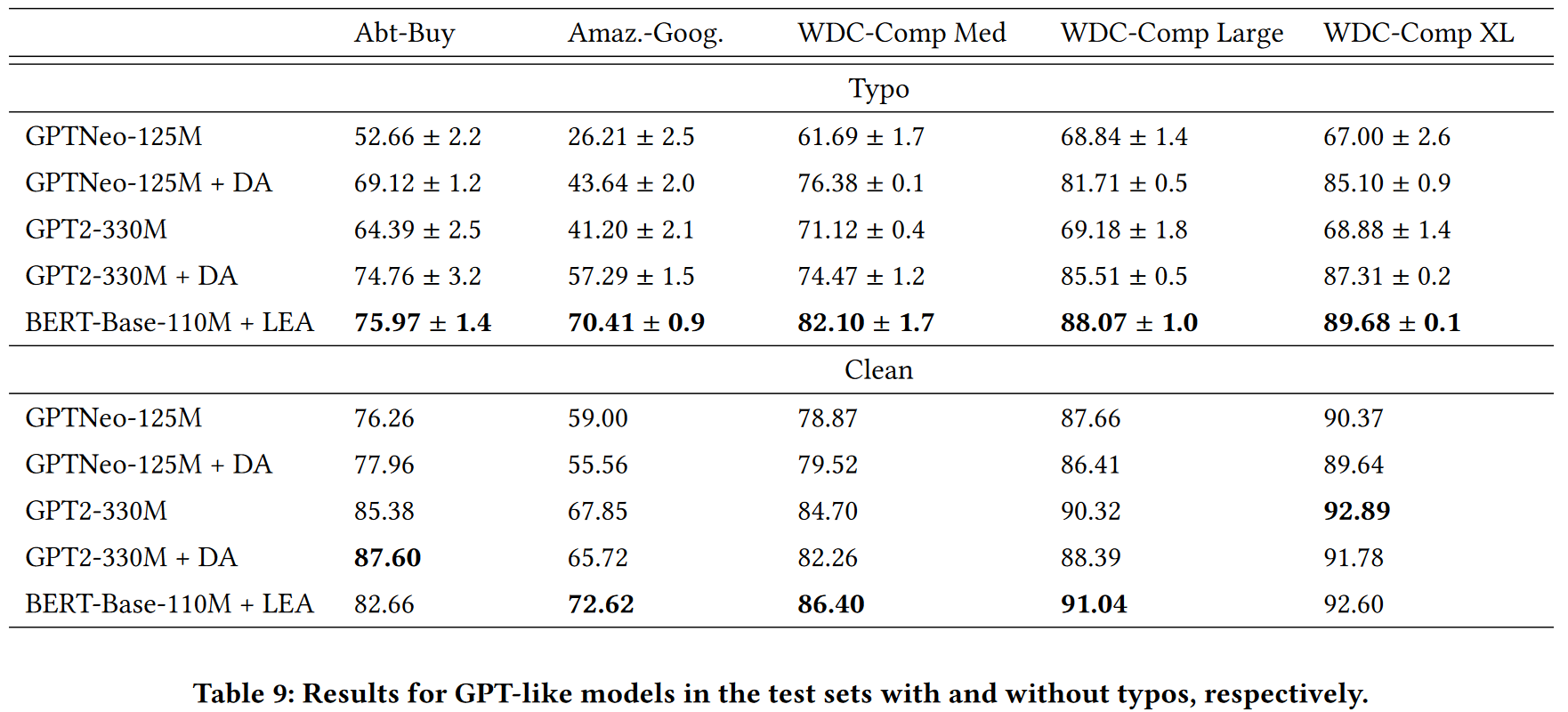
Larger dataset
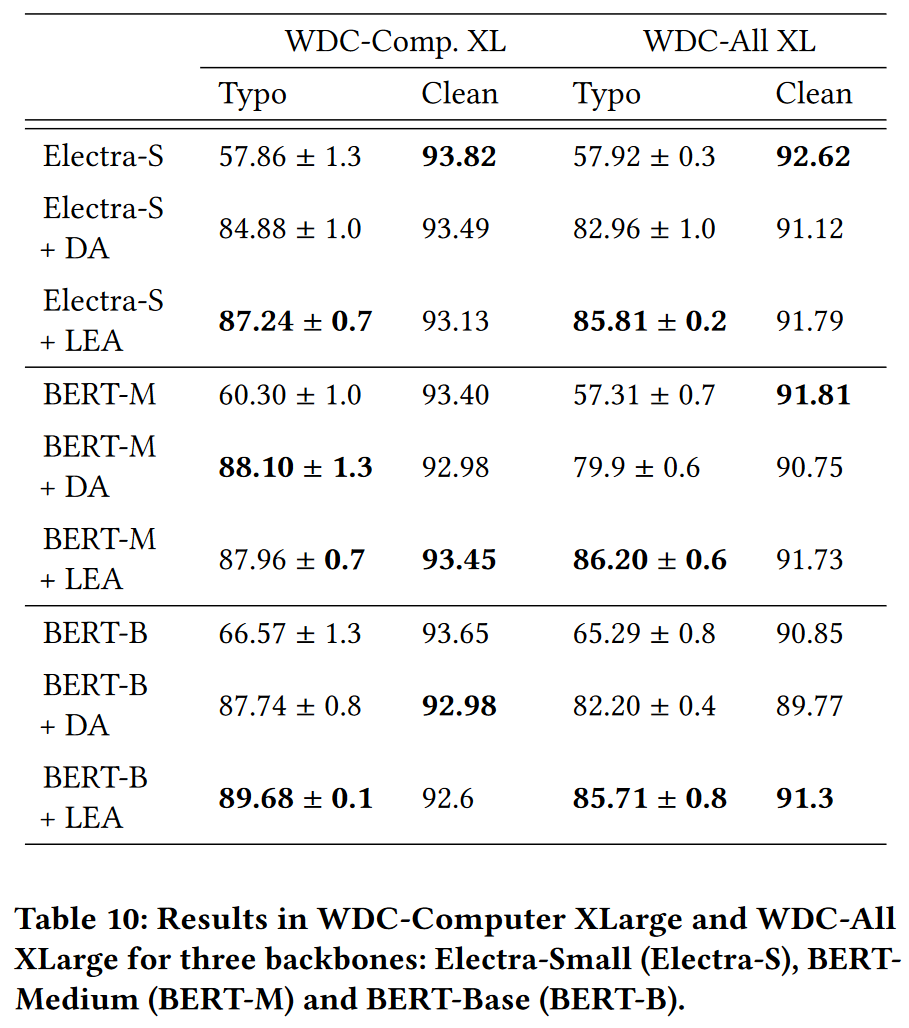
BERT-M + DA 在 WDC-Comp.XL 性能超过了 LEA, 但是标准差较大.