这节课中介绍了训练神经网络的第二部分,包括学习率曲线,超参数优化,模型集成,迁移学习
-
训练神经网络2
- 学习率曲线
- 超参数优化
- 模型集成
- 迁移学习
学习率曲线
在训练神经网络时,一个常见的思路就是刚开始迭代的时候学习率较大,然后随着迭代次数的增加,学习率逐渐下降,下面我们就来介绍几种学习率下降的方法:
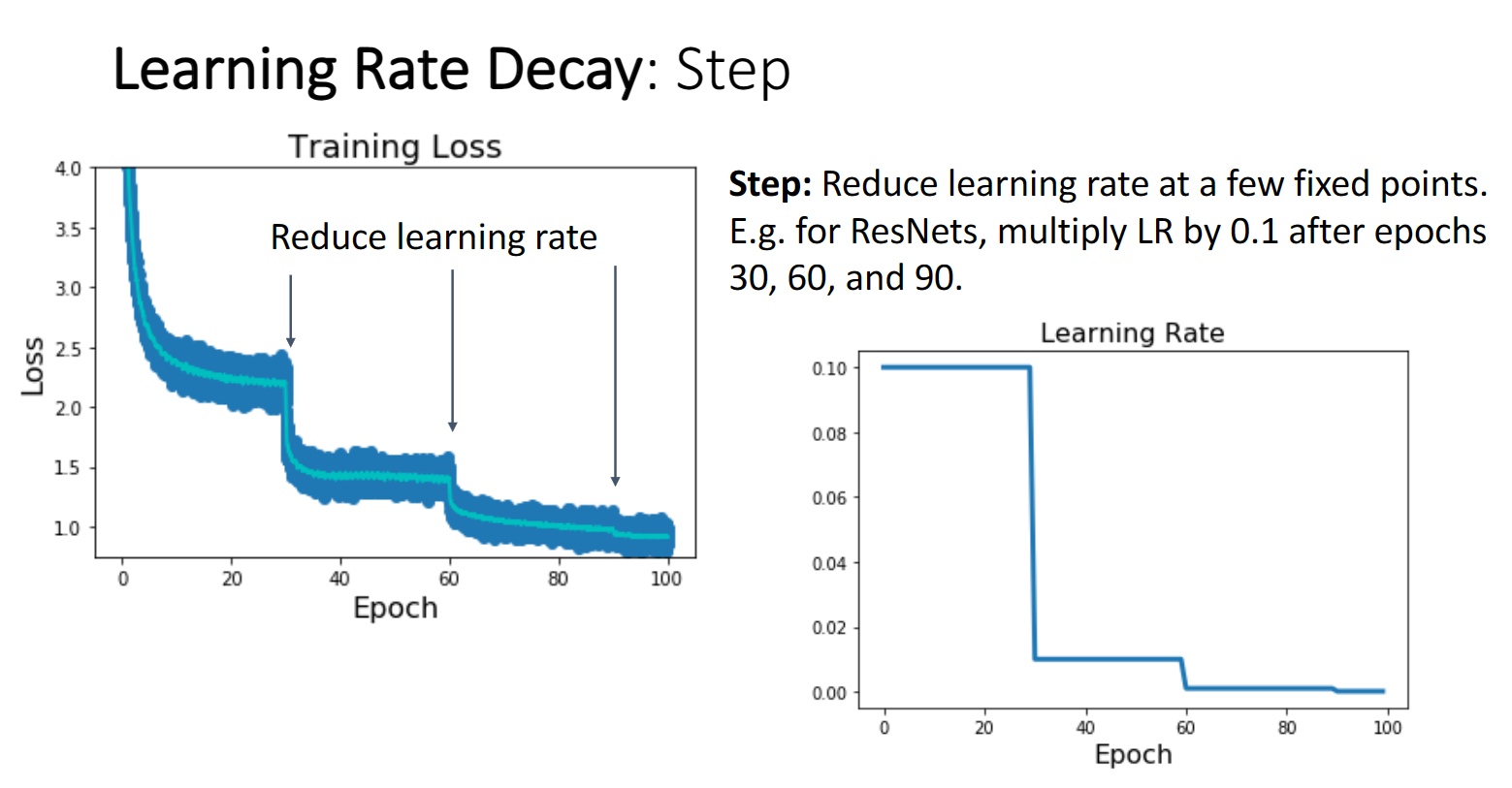
第一种方法是我们在某些特定的迭代节点,将学习率乘以某个值比如0.1,这种方法显然又引入了更多的超参数,我们不想这样做,所以又设计了其它的下降曲线
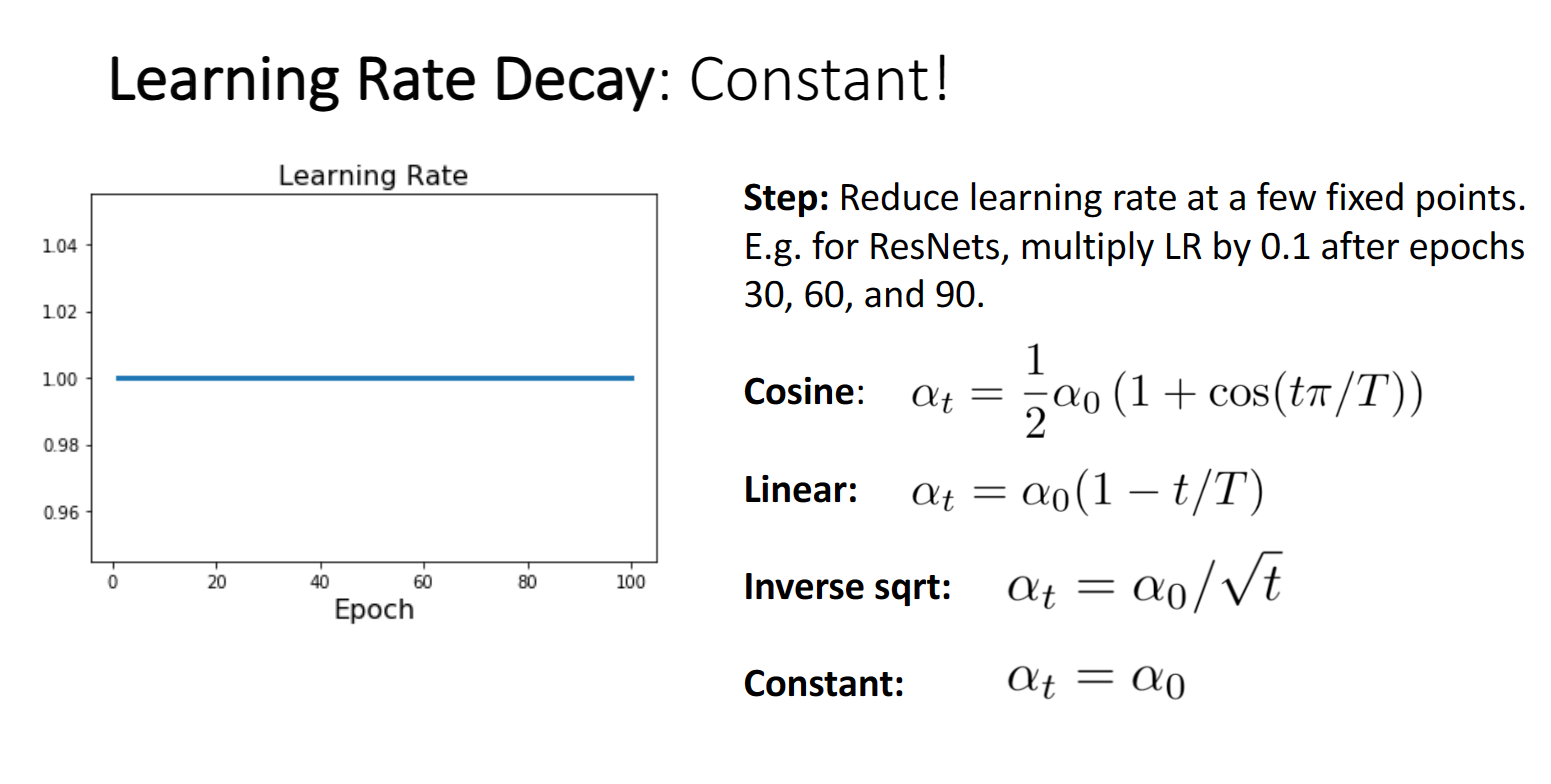
比如上图的cos linear 等等 我们有时会发现保持学习率不变也是个不错的选择
实际上不同下降方法之间没有明显的对比统计,大多是根据不同领域习惯选择不同方法,比如计算机视觉用cos,大规模自然语言处理用linear等
在训练的时候,我们应该在发现验证集上准确率下降的时候就停止训练:
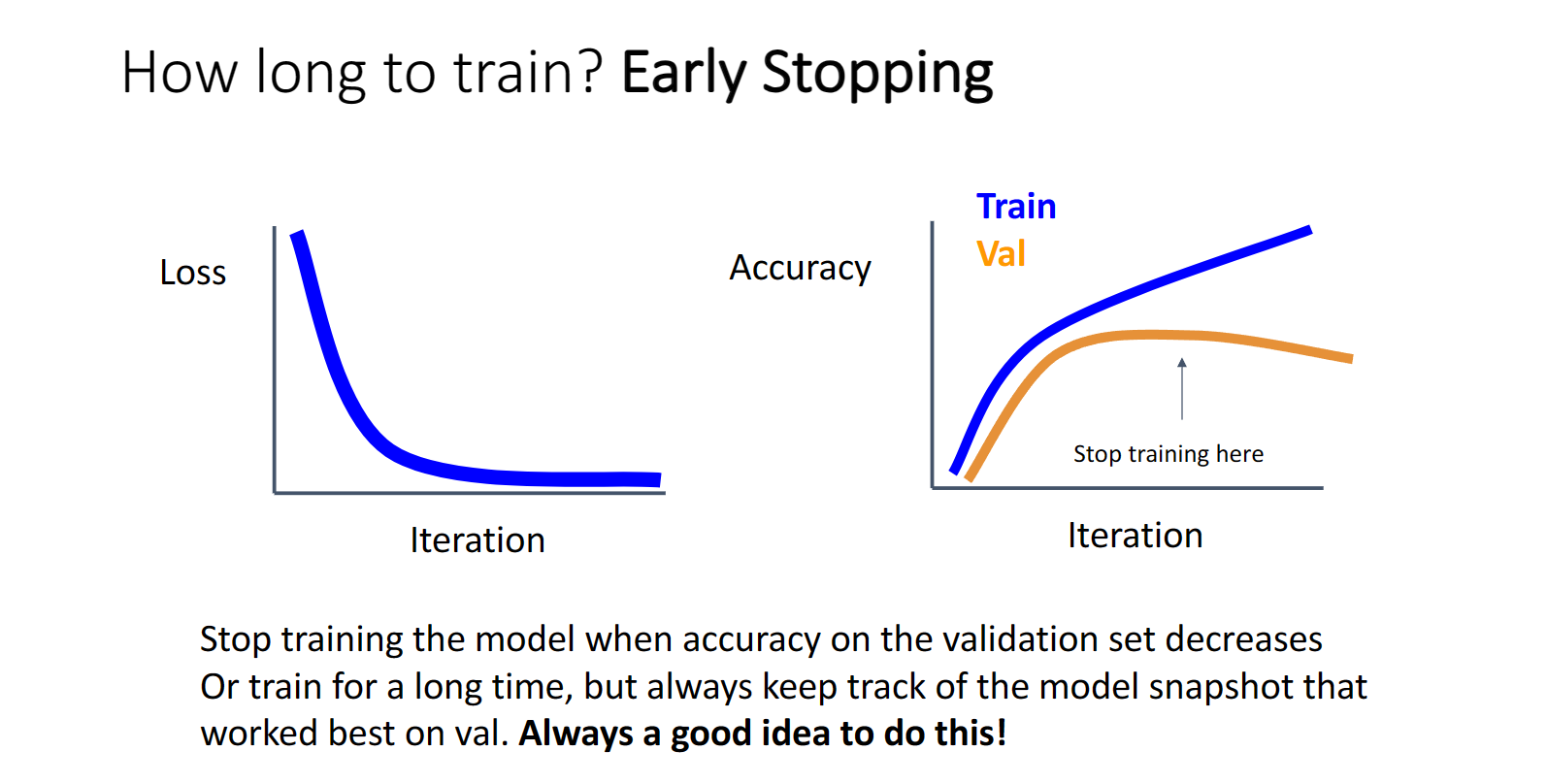
超参数优化
在训练神经网络的时候,在不同的超参数之间选择,我们常常会采用网格搜索,将不同的值排列组合,然后去训练

有时我们也会选择随机搜索,在设置的范围内随机选取相应的超参数的值:

在实际应用中往往随机搜索更好,从下图可以看出,最上面的绿色曲线表示准确率,网格搜索只能表示曲线上固定的几个值,而随机搜索引入了更多的随机性,从而可能得到更好的结果:
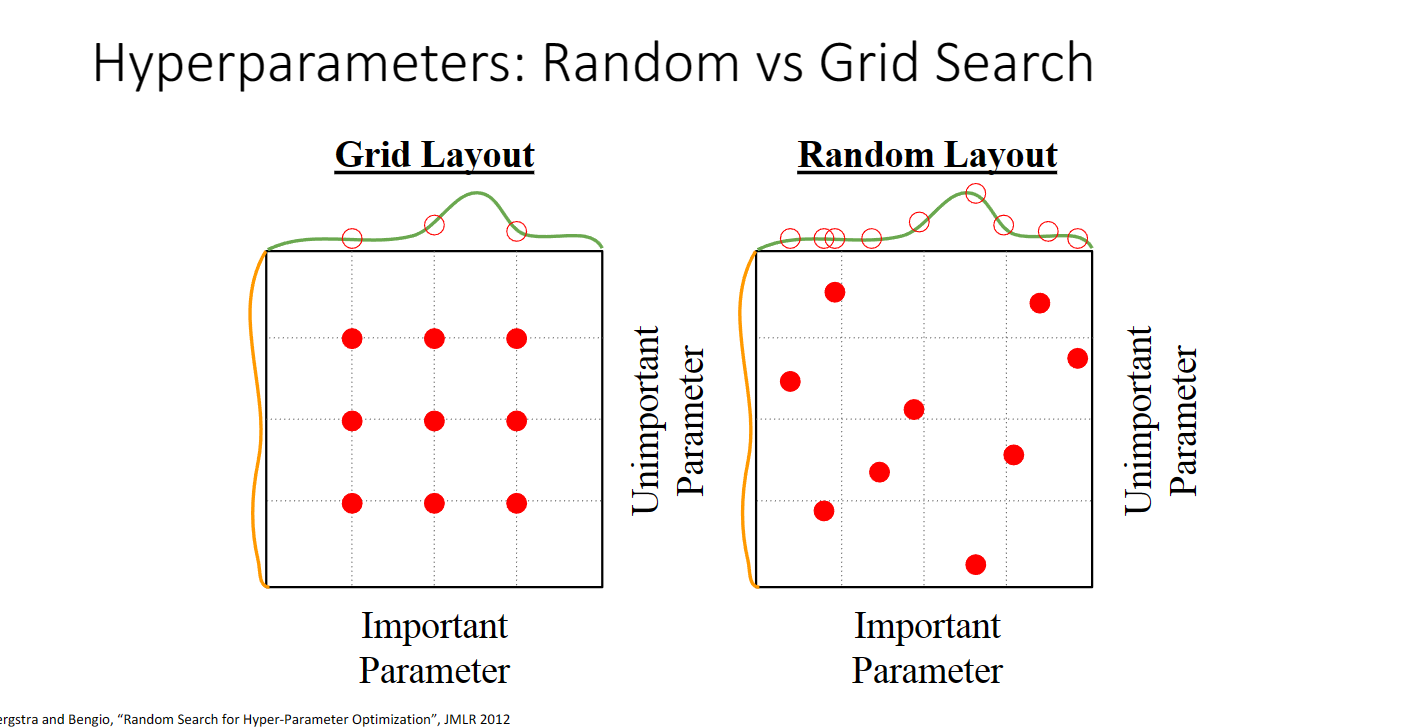
在选择超参数的过程中,我们一般有具体的流程:

第一步我们在什么都没有设置的情况下,可以先运行一下模型,看看损失是否正常,比如我们采用softmax函数输出c个类的得分,它的初始损失应该是log(c)
第二步我们先在几个比较小的样本集数据中训练我们的神经网络,调整网络架构,调整学习率与权重,注意不使用正则化方法,让我们的模型在小数据集上能达到100%的准确度,通过画迭代次数与loss的曲线观察,如果损失一直不下降,说明我们采用的学习率太小,如果损失突然下降到0或者损失爆炸,说明我们采用的学习率太大,并且上述两种情况都说明我们的初始化很糟糕
第三步我们根据前几步确定的结构,在此基础上使用权重衰减,采用不同的学习率,找到一个学习率,能在固定的迭代步骤内,使得损失下降幅度最大:

第四步我们选择第三步中的一些学习率与权重衰减,迭代几次,找出比较好的模型用于第五步,迭代更长时间,然后我们画出相关的学习曲线(损失与迭代次数的统计图,训练集与验证集在不同迭代次数上的统计图)作进一步的观察:

对于损失与迭代次数的统计图
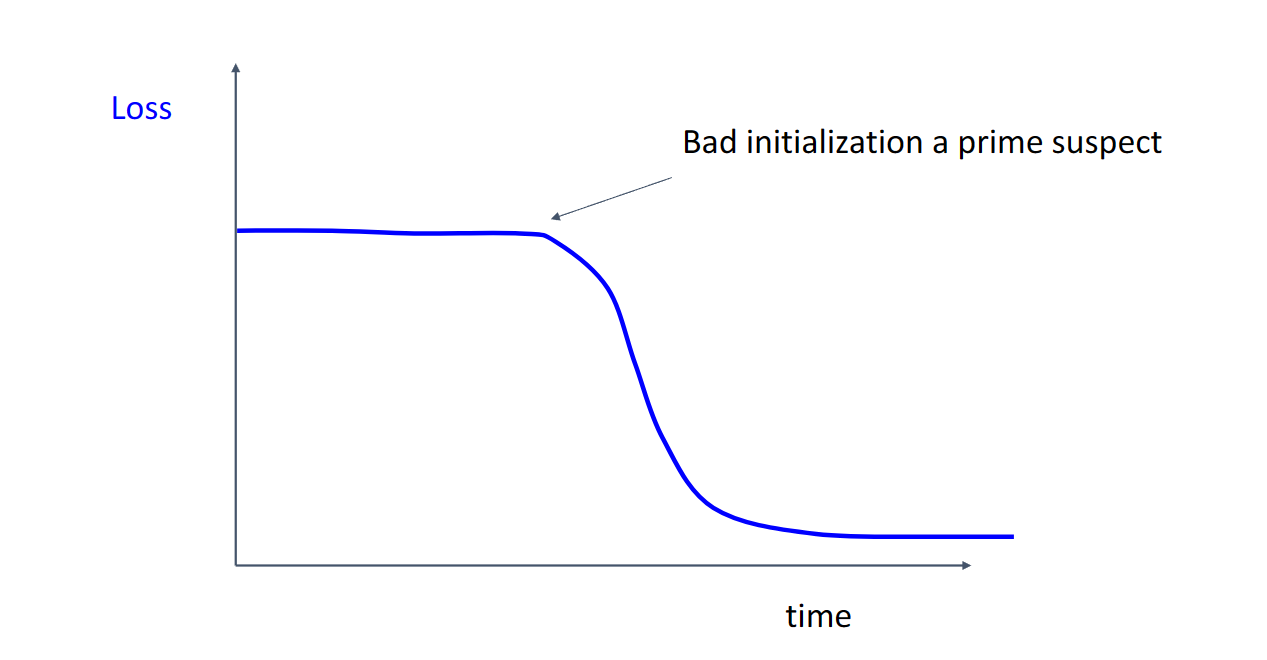
这种在一段迭代次数内损失不下降说明我们初始化较为糟糕
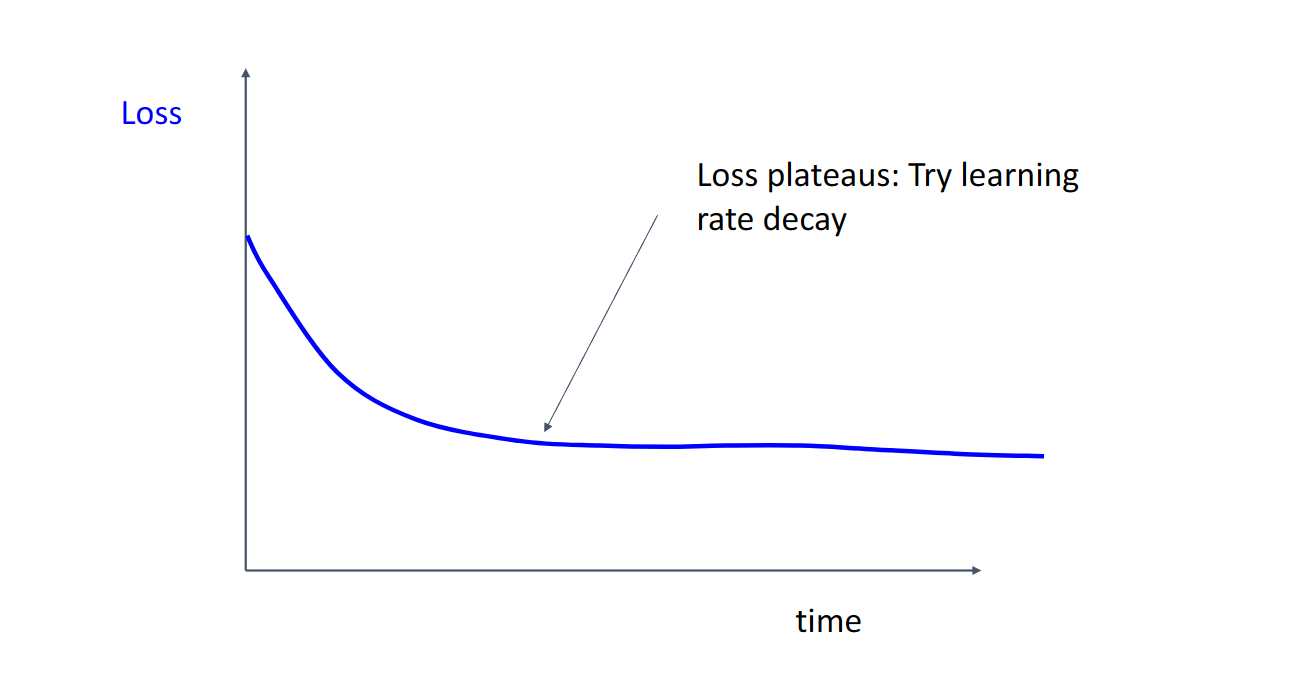
这种出现损失平原的情况说明我们可以尝试学习率下降的方法
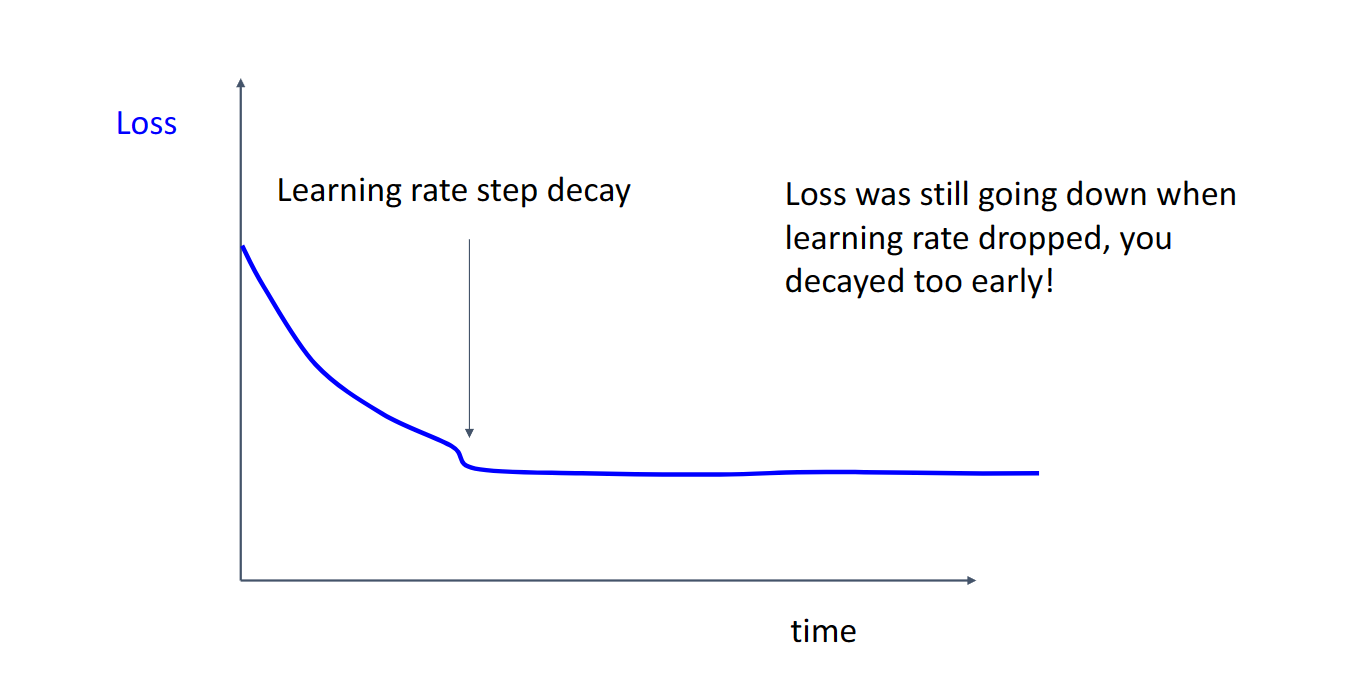
当学习率下降损失依然下降,说明我们采用的下降方法下降的太早了
对于训练集与验证集在不同迭代次数上的统计图
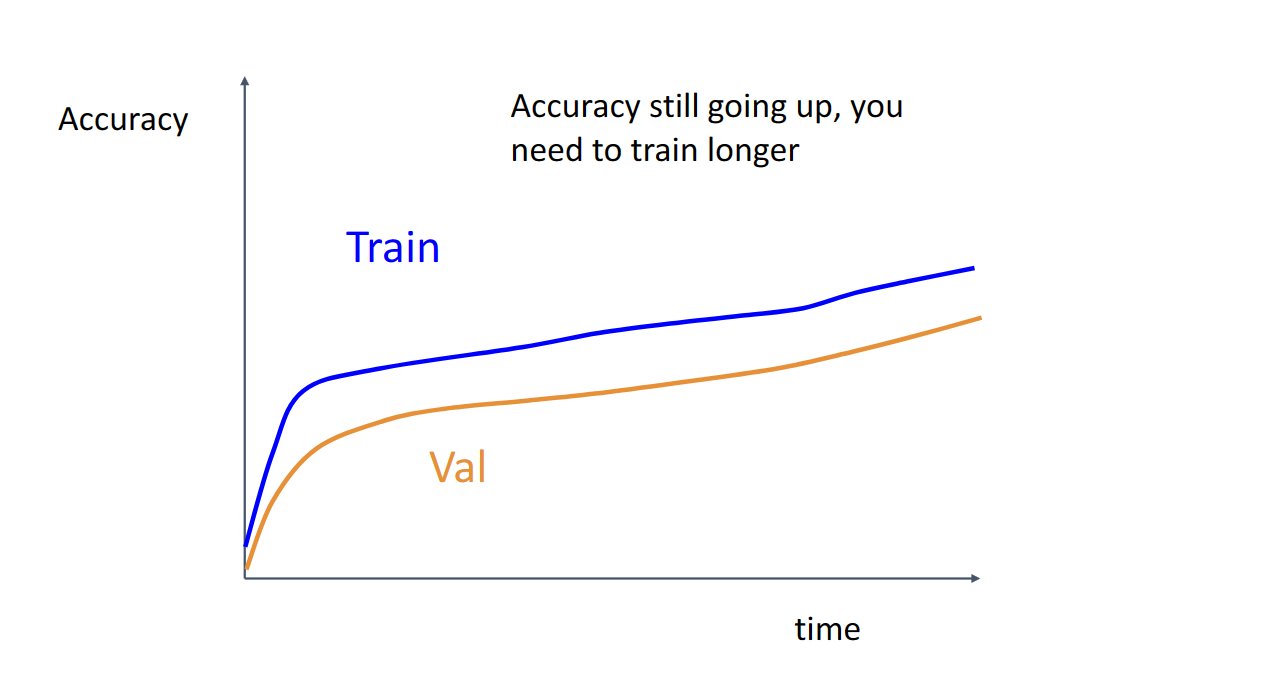
一直上升说明我们还可以训练更长时间
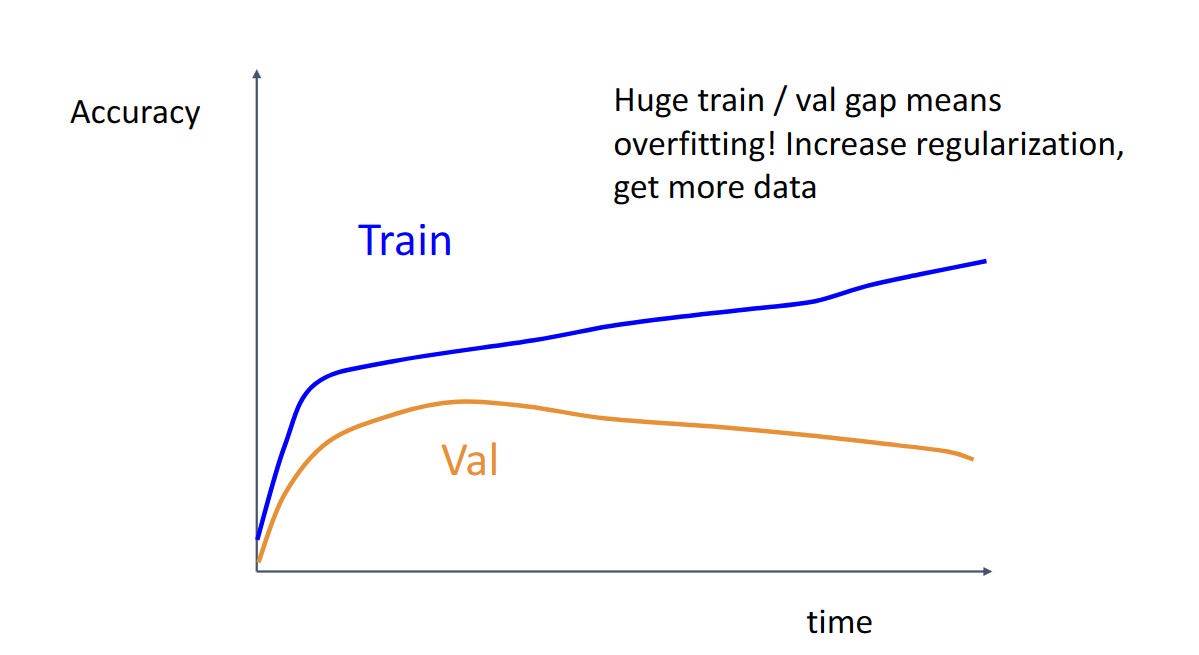
这种差异过大的曲线说明我们过拟合了,需要提升正则化强度或者引入更多数据
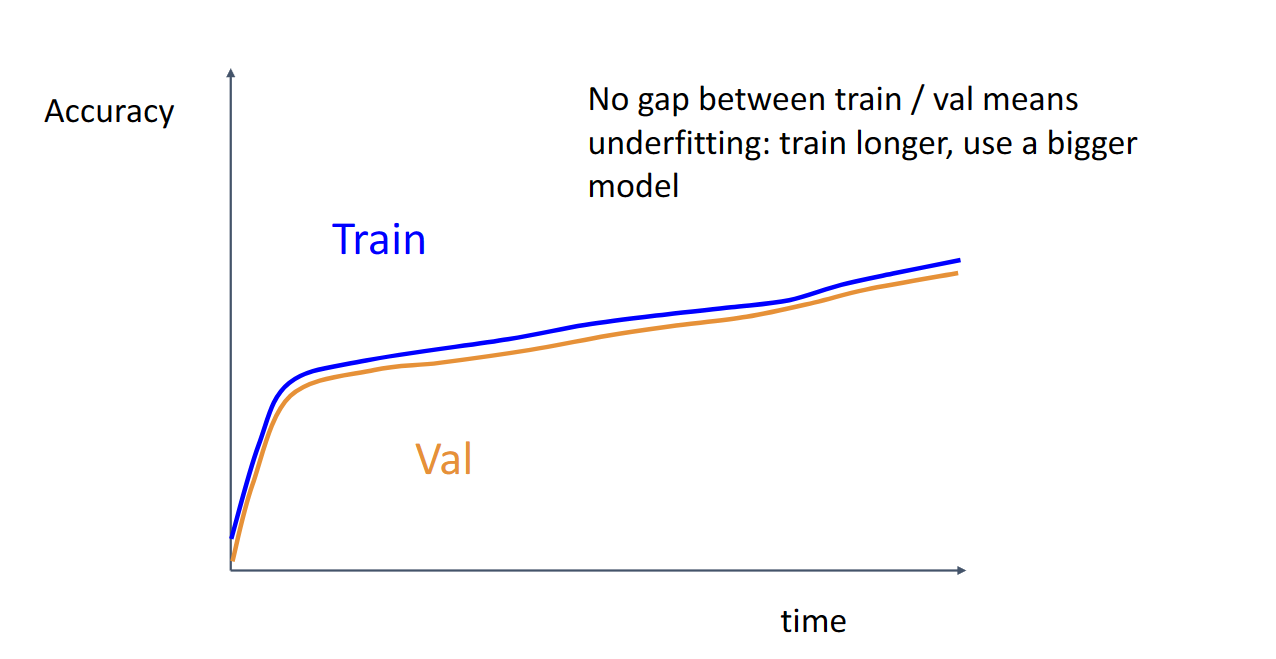
这种差异过小的曲线说明我们under fitting,需要训练更长时间,选择更复杂的模型
模型集成
模型集成常见的思路就是训练不同的模型,然后取它们结果的平均值:

我们也可以采用一个模型,在不同的训练时间输出不同的结果,再取平均值,采用循环学习率很有利于这种snapshot集成的方法:
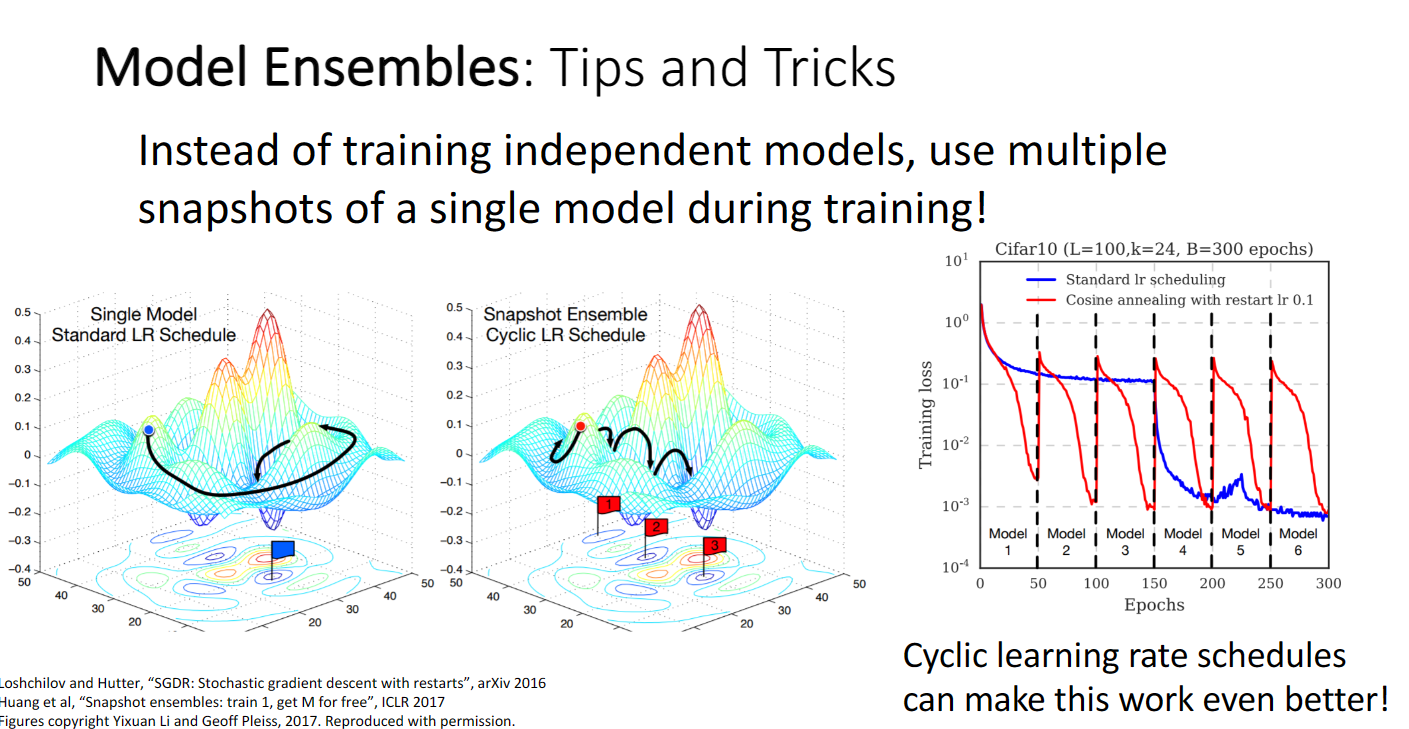
同时我们也可以将这种思想应用于参数向量:

迁移学习
迁移学习是为了解决数据量不足的问题

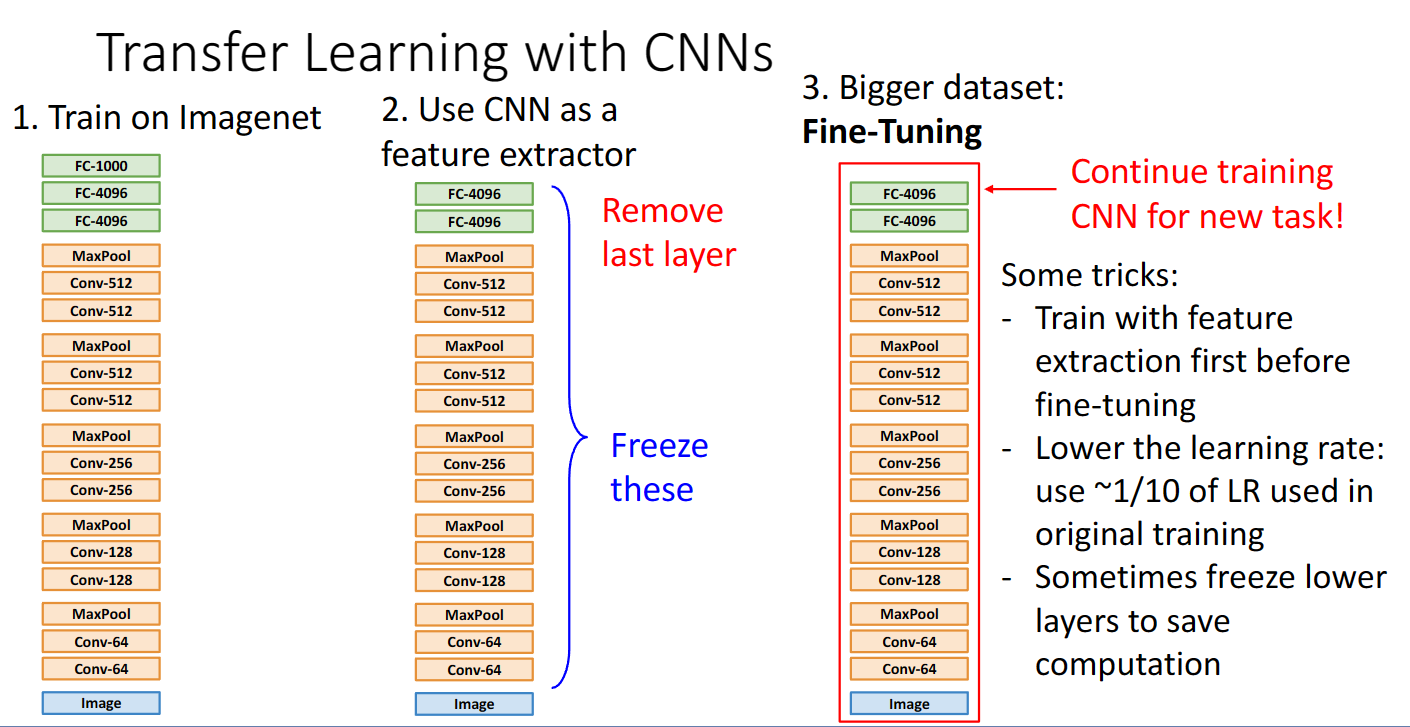
先在给定的数据集上使用某种卷积网络训练图像数据,然后去除最后一层不获取预测得分,使用这个卷积网络作为特征向量提取器,冻结之前训练的层,然后再使用其它方法输出结果
比如右图2009年专门为数据集设计的神经网络
其余两个是在VGG上预训练 然后使用svm或者逻辑回归输出结果 得到的效果就比专门设计的要好
如果我们有更大的数据集,我们可以对cnn网络架构进行进一步的训练,使其能完成更多类型的工作
事实证明cnn网络结构的优化可以为许多下游的工作带来提升
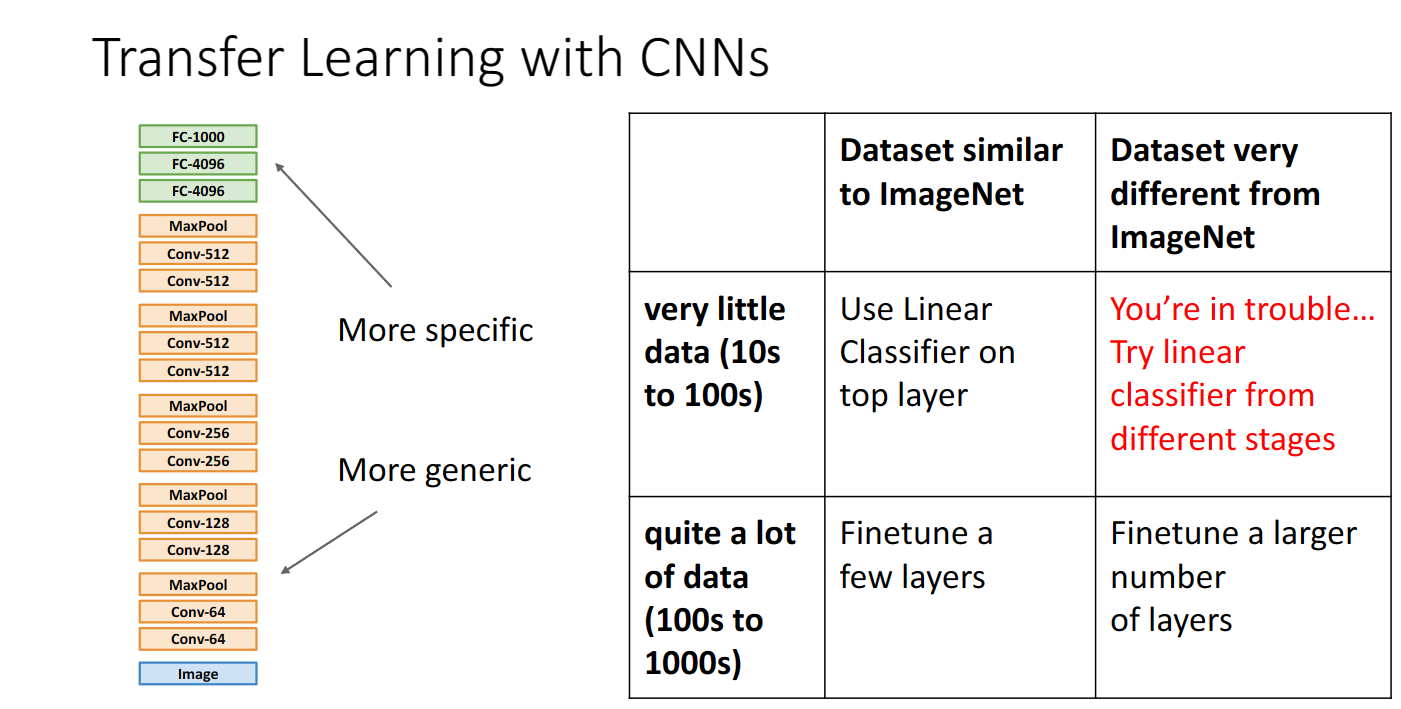
上图说明了我们尝试在不同的数据集上应用cnn进行迁移学习需要进行的操作,假如数据集与imagenet相似,并且数据量较小,我们可以使用线性分类器输出结果,假如数据量较大,我们可以利用这些数据微调一些层,假如数据量较大并且与imagenet数据集不想死,我们需要在更多层上进行微调,如果数据量较小,我们就需要更多的尝试
下面两张图展现了这种迁移学习方法的广泛应用:
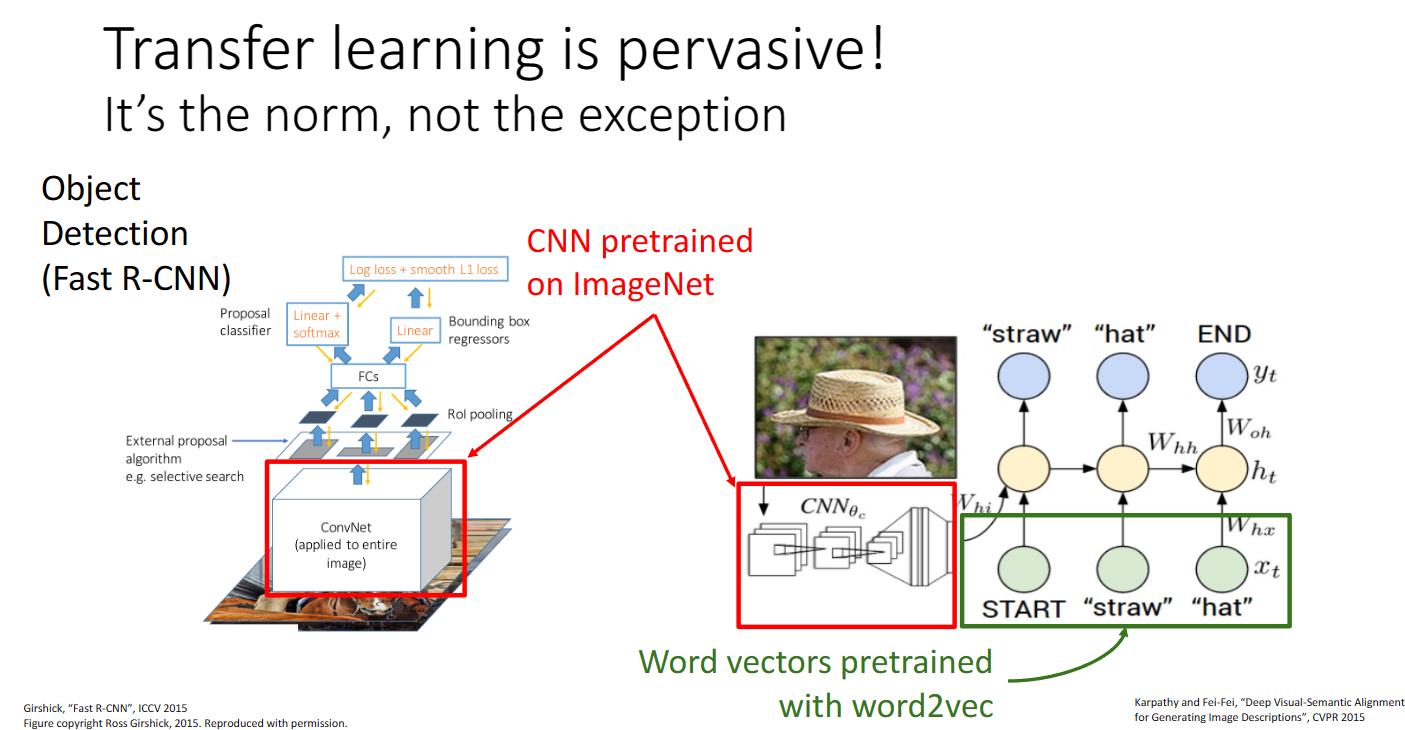

可以在物体检测 语言建模等方面应用

但是对于迁移学习也存在一些疑问,有人指出这种方法并没有比从头开始设计网络的方法好很多,小哥的建议是如果有充足的数据和算力,我们可以从头开始设计并且调整网络,大多数情况下使用预训练的网络加上微调步骤十分高效







